In numerical analysis and linear algebra, lower–upper (LU) decomposition or factorization factors a matrix as the product of a lower triangular matrix and an upper triangular matrix. The product sometimes includes a permutation matrix as well. LU decomposition can be viewed as the matrix form of Gaussian elimination. Computers usually solve square systems of linear equations using LU decomposition, and it is also a key step when inverting a matrix or computing the determinant of a matrix

LU Decomposition

Assume A is a square matrix, LU decomposition is transforming matrix A to be product of two matrices called L and U as below:

A=LU

{\displaystyle {\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{bmatrix}}={\begin{bmatrix}l_{11}&0&0\\l_{21}&l_{22}&0\\l_{31}&l_{32}&l_{33}\end{bmatrix}}{\begin{bmatrix}u_{11}&u_{12}&u_{13}\\0&u_{22}&u_{23}\\0&0&u_{33}\end{bmatrix}}.}

Example

Here is a square 2×2 matrix

{\displaystyle {\begin{bmatrix}4&3\\6&3\end{bmatrix}}={\begin{bmatrix}l_{11}&0\\l_{21}&l_{22}\end{bmatrix}}{\begin{bmatrix}u_{11}&u_{12}\\0&u_{22}\end{bmatrix}}.}

To finding L and U matrices, one approach is to solve below equation system

{\displaystyle {\begin{aligned}l_{11}\cdot u_{11}+0\cdot 0&=4\\l_{11}\cdot u_{12}+0\cdot u_{22}&=3\\l_{21}\cdot u_{11}+l_{22}\cdot 0&=6\\l_{21}\cdot u_{12}+l_{22}\cdot u_{22}&=3.\end{aligned}}}

we applied lower and upper triangle limits to equations to be able to solve it so we have below

{\displaystyle {\begin{aligned}l_{21}&=1.5\\u_{11}&=4\\u_{12}&=3\\u_{22}&=-1.5\end{aligned}}}

By replacing values in matrices we will have

{\displaystyle {\begin{bmatrix}4&3\\6&3\end{bmatrix}}={\begin{bmatrix}1&0\\1.5&1\end{bmatrix}}{\begin{bmatrix}4&3\\0&-1.5\end{bmatrix}}.}

Matlab Code

create LU.m file in copy below code and save it

function [ L, U ] = LU(A)
% check if A is square
sz = size(A);
if sz(1)~=sz(2)
    fprintf('A is not square !\n');
    clear x;
    return;
end
n = sz(1);
L = eye(n); 
% create matrix that all components are 1 (for starting)
P = eye(n);
U = A;
for i=1:sz(1)
    % decrease row   
    if U(i,i)==0
        maximum = max(abs(U(i:end,1)));
        for k=1:n
           if maximum == abs(U(k,i))
               temp = U(1,:);
               U(1,:) = U(k,:);
               U(k,:) = temp;
 
               temp = P(:,1);
               P(1,:) = P(k,:);
               P(k,:) = temp;
           end
        end
 
    end
    if U(i,i)~=1
        temp = eye(n);
        temp(i,i)=U(i,i);
        L = L * temp;
        U(i,:) = U(i,:)/U(i,i);
    end
    if i~=sz(1)
        for j=i+1:length(U)
            temp = eye(n);
            temp(j,i) = U(j,i);
            L = L * temp;
            U(j,:) = U(j,:)-U(j,i)*U(i,:);
 
        end
    end
end
end

Usage:

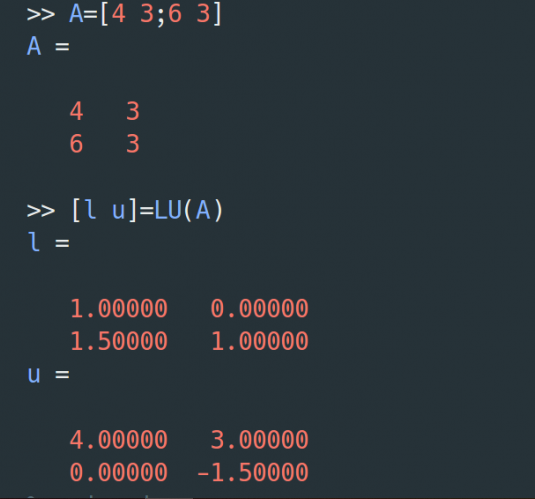
after saving above file, in command window you can use it

A=[4 5;6 8]
[l u]=LU(A)